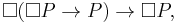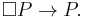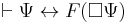Löb's theorem
In mathematical logic, Löb's theorem states that in a theory with Peano arithmetic, for any formula P, if it is provable that "if P is provable then P", then P is provable. I.e.
- if
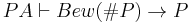 , then
, then 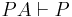
where Bew(#P) means that the formula P with Gödel number #P is provable.
Löb's theorem is named for Martin Hugo Löb, who formulated it in 1955.
Contents |
Löb's theorem in provability logic
Provability logic abstracts away from the details of encodings used in Gödel's incompleteness theorems by expressing the provability of  in the given system in the language of modal logic, by means of the modality
in the given system in the language of modal logic, by means of the modality 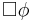 .
.
Then we can formalize Löb's theorem by the axiom
known as axiom GL, for Gödel-Löb. This is sometimes formalised by means of an inference rule that infers
from
The provability logic GL that results from taking the modal logic K4 and adding the above axiom GL is the most intensely investigated system in provability logic.
Modal Proof of Löb's theorem
Löb's theorem can be proved within modal logic using only some basic rules about the provability operator plus the existence of modal fixed points.
Modal Formulas
We will assume the following grammar for formulas:
- If
 is a propositional variable, then
is a propositional variable, then  is a formula.
is a formula. - If
 is a propositional constant, then
is a propositional constant, then  is a formula.
is a formula. - If
 is a formula, then
is a formula, then 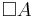 is a formula.
is a formula. - If
 and
and  are formulas, then so are
are formulas, then so are 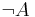 ,
, 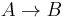 ,
, 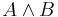 ,
, 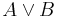 , and
, and 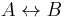
A modal sentence is a modal formula that contains no propositional variables. We use 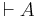 to mean
to mean  is a theorem.
is a theorem.
Modal Fixed Points
If 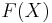 is a modal formula with only one propositional variable
is a modal formula with only one propositional variable  , then a modal fixed point of
, then a modal fixed point of 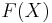 is a sentence
is a sentence 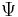 such that
such that
We will assume the existence of such fixed points for every modal formula with one free variable. This is of course, not an obvious thing to assume, but if we interpret  as provability in Peano Arithmetic, then the existence of modal fixed points is in fact true.
as provability in Peano Arithmetic, then the existence of modal fixed points is in fact true.
Modal Rules of Inference
In addition to the existence of modal fixed points, we assume the following rules of inference for the provability operator  :
:
- From
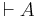 conclude
conclude  : Informally, this says that if A is a theorem, then it is provable.
: Informally, this says that if A is a theorem, then it is provable. 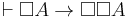 : If A is provable, then it is provable that it is provable.
: If A is provable, then it is provable that it is provable.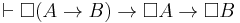 : This rule allows you to do modus ponens inside the provability operator. If it is provable that A implies B, and A is provable, then B is provable.
: This rule allows you to do modus ponens inside the provability operator. If it is provable that A implies B, and A is provable, then B is provable.
Proof of Löb's theorem
- Assume that there is a modal sentence
 such that
such that 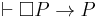 . Roughly speaking, it is a theorem that if
. Roughly speaking, it is a theorem that if  is provable, then it is, in fact true. This is a claim of soundness.
is provable, then it is, in fact true. This is a claim of soundness. - Let
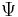 be a sentence such that
be a sentence such that 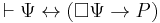 . The existence of such a sentence follows the existence of a fixed point of the formula
. The existence of such a sentence follows the existence of a fixed point of the formula 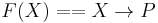 .
. - From 2, it follows that
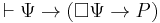 .
. - From rule of inference 1, it follows that
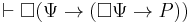 .
. - From 4 and rule of inference 3, it follows that
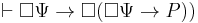 .
. - From rule of inference 3, it follows that
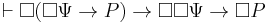
- From 5 and 6, it follows that

- From rule of inference 2, it follows that
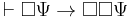
- From 7 and 8, it follows that

- From 1 and 9, it follows that
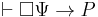
- From 10 and 2, it follows that
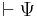
- From 11 and rule of inference 1, it follows that

- From 12 and 10, it follows that
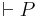
References
- Hinman, P. (2005). Fundamentals of Mathematical Logic. A K Peters. ISBN 1-568-81262-0.
- Boolos, George S. (1995). The Logic of Provability. Cambridge University Press. ISBN 0-521-48325-5.